ベン図を「資格の強さ」で理解する
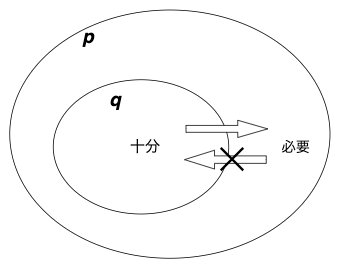
命題と論証の問題は、「包含関係」「矢印の向き」「必要条件と十分条件の識別」の3つを理解することで解ける。
それらをすべて表したのが上図であり、これさえ書ければ、すべて解ける。
この図の書き方をマスターしよう。
まず、敷地pの中に、鍵のかかった部屋qがあると考えてほしい。
- qの住人達は、自由に外に出ることもできるから、右向きの矢印が成り立つ。
- 外の人達は、qに入ることができないので、左向きの矢印は成り立たない。
これで、矢印とバツ印を書き込むことができる。
次に、qをYouTubeの有料会員に置き換えてみよう。
- すべてのYouTube視聴者(p)は、動画の視聴などの「必要」なサービスを受けられる。
- 一部の有料会員(q)だけが、広告の非表示などの「十分」なサービスを受けられる。
これにより、図の十分と必要を書き込むことができ、次のことが言える。
「pはqの必要条件であり、qはpの十分条件である」
これにて、「包含関係」「矢印の向き」「必要条件と十分条件の識別」のすべてを対応させて、理解することができる。
ベン図を「階級の高さ」で理解する
先ほどのベン図が、実は上から見下ろした山だったのだと考えてみる。ベン図が等高線の束に見えてくるだろう。
山を横から見て、図を書き直したものが次図である。
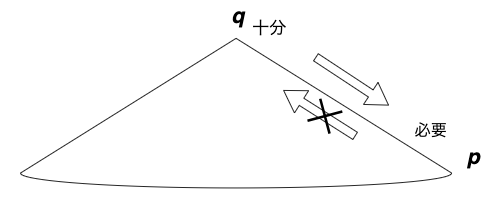
山頂付近の湖を源流として、上流、下流へと水が流れていく。流れてきた水を、下流に住む村人が生活用水として使っていると考えてみよう。
上流には「十分」量の水があり、下流で「必要」量の水を使う。図で表すと、次のようになる。

すると、矢印の根本が十分条件、矢印の先端が必要条件になる。
この考え方は、「矢印の向き」から、「必要条件と十分条件の識別」をするのに役立つ。
実際に、問題が解けるか確かめてみよう
「矢印の向き」から「必要か十分か」判断するとき
問1. abが有理数であることは、a,bともに有理数であるための__条件である。
解答)
a,bがともに有理数→abが有理数は真
abが有理数→a,bがともに有理数は偽(反例:a=b=√2)
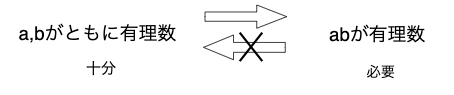
矢印の根本が十分条件、矢印の先端が必要条件であることを思い出せば、答えは必要条件であると分かる。
「包含関係」から「必要か十分か」判断するとき
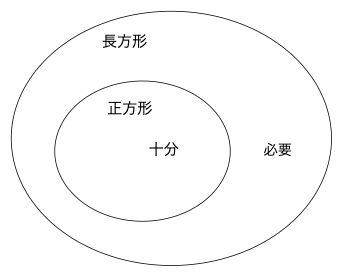
問2. 四角形ABCDが正方形であることは、四角形ABCDが長方形であるための__条件である。
解答)
矢印でも判断できるが、図を描けば一瞬だ。
正方形とは、特殊な長方形であるから、長方形という集合の中に含まれる。
内側が十分、外側が必要であることを思い出せば、答えは十分条件と分かる。
「包含関係」から「矢印の向き」を判断するとき
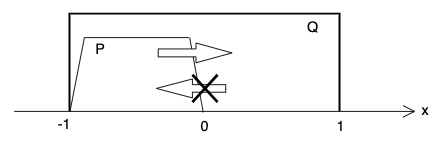
問3. P→Qの真偽を判定せよ。
P:-1<x<0
Q:-1≦x≦1とする。
解答)
数直線上に図示すると、下図のようになり、PはQに含まれる。
包含関係の内側から、外側へ矢印が伸びることを思い出せば、答えは真であると分かる。